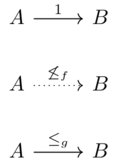Chapter 2: Resource theories

Getting from A to B(1)
Symmetric monoidal preorders(40)
Definition and first examples(9)

The notation for monoidal product and unit may vary depending on context. \(I, \otimes\) are defaults but it may be best to use \((0,+),(1,*),(true, \land)\) (etc.)

Symmetric monoidal structure on a preorder(1)

A symmetric monoidal structure on a preorder \((X, \leq)\)

  • Two additional constituents:

    1. A monoidal unit \(I \in X\)

    2. A monoidal product \(X \times X \xrightarrow{\otimes} X\)

  • Satisfying the following properties:

    1. Monotonicity: \(\forall x_1,x_2,y_1,y_2 \in X: x_1 \leq y_1 \land x_2 \leq y_2 \implies x_1 \otimes x_2 \leq y_1 \otimes y_2\)

    2. Unitality: \(\forall x \in X: I \otimes x = x = x \otimes I\)

    3. Associativity: \(\forall x,y,z \in X: (x \otimes y) \otimes z = x \otimes (y\otimes z)\)

    4. Symmetry: \(\forall x,y \in X: x \otimes y = y \otimes x\)

Linked by

Weak monoidal structure on a preorder(1)

A weak monoidal structure on a preorder \((X, \leq)\)

Definition is identical to a symmetric monoidal structure, replacing all \(=\) signs with \(\cong\) signs.

Discrete SMP(1)

  • A monoid is a set \(M\) with a monoid unit \(e \in M\) and associative monoid multiplication \(M \times M \xrightarrow{\star} M\) such that \(m \star e=m=e \star m\)

  • Every set \(S\) determines a discrete preorder: \(\mathbf{Disc}_S\)

  • It is easy to check if \((M,e,\star)\) is a commutative monoid then \((\mathbf{Disc}_M, =, e, \star)\) is a symmetric monoidal preorder.

Linked by

Poker hands(1)

  • Let \(H\) be the set of all poker hands, ordered by \(h \leq h'\) if \(h'\) beats or ties hand \(h\).

  • One can propose a monoidal product by assigning \(h_1 \otimes h_2\) to be “the best hand one can form out of the ten cards in \(h_1 \bigcup h_2\)"

  • This proposal will fail monotonicity with the following example:

    • \(h_1 := \{2\heartsuit, 3\heartsuit,10 \spadesuit,J\spadesuit,Q\spadesuit\} \leq i_1 := \{4\spadesuit,4\spadesuit,6\heartsuit,6\diamondsuit,10\diamondsuit\}\)

    • \(h_2 := \{2\diamondsuit,3\diamondsuit,4\diamondsuit,K\spadesuit,A\spadesuit\} \leq i_2 := \{5\spadesuit,5\heartsuit,7\heartsuit,J\diamondsuit,Q\diamondsuit\}\)

    • \(h_1 \otimes h_2=\{10\spadesuit,J\spadesuit,Q\spadesuit,K\spadesuit,A\spadesuit\} \not \leq i_2 \otimes i_2 = \{5\spadesuit, 5\heartsuit,6\heartsuit,6\diamondsuit,Q\diamondsuit\}\)

Exercise 2-5(2)

Consider the reals ordered by our normal \(\leq\) relation. Do \((1,*)\) as unit and product for a symmetric monoidal structure?

Solution(1)

No, monotonicity fails: \(x_1\leq y_1 \land x_2 \leq y_2 \not \implies x_1x_2 \leq y_1y_2\) (Counterexample: \(x_1=x_2=-1, y_1=y_2=0\))

Exercise 2-8(2)

Check if \((M,e,\star)\) is a commutative monoid then \((\mathbf{Disc}_M, =, e, \star)\) is a symmetric monoidal preorder, as described in this example.

Solution(1)

  • Monotonicity is the only tricky one, and is addressed due to the triviality of the discrete preorder.

    • We can replace \(x \leq y\) with \(x \leq x\) because it is a discrete preorder.

    • \(x_1 \leq x_1 \land x_2 \leq x_2 \implies x_1 \otimes x_2 \leq x_1 \otimes x_2\)

    • \(True \land True \implies True\) is vacuously true due to reflexivity of preorder.

  • Unitality/associativity comes from unitality/associativity of monoid

  • Symmetry comes from commutitivity of monoid.

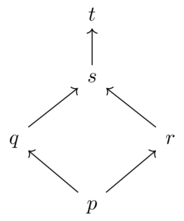
Introducing wiring diagrams(3)
Exercise 2-20(2)

  • Given the assertions the interior of this wiring diagram:

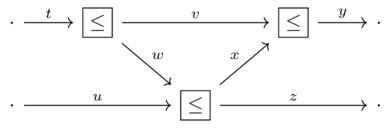
  • Prove that the conclusion follows using the rules of symmetric monoidal preorders

    • Make sure to use reflexivity and transitivity

  • How do you know that symmetry axiom does not need to be invoked?

Solution(1)

  • Assertions:

    • \(t \leq v+w\)

    • \(w+u \leq x+z\)

    • \(v+x \leq y\)

  • Conclusion: \(t+u \leq y+z\)

  • Proof:

    • \((t)+(u) \leq (v+w)+(u)\) - from monotonicity and reflexivity of u

    • \(= v+(w+u)\) - associativity

    • \(\leq v+(x+z)\) - monotonicity and reflexivity of v

    • \(= (v+x)+z\) - associativity

    • \(\leq y+z\) - monotonicity and reflexivity of z

  • Symmetry was not needed because the diagram had no crossing wires.

  • Visual representations for building new relationships from old.

  • For a preorder without a monoidal structure, we can only chain relationships linearly (due to transitivity).

  • For a symmetric monoidal structure, we can combine relationships in series and in parallel.

  • Call boxes and wires icons

  • Any element \(x \in X\) can be a label for a wire. Given x and y, we can write them as two wires in parallel or one wire \(x \otimes y\); these are two ways of representing the same thing.

  • Consider a wire labeled \(I\) to be equivalent to the absence of a wire.

  • Given a \(\leq\) block, we say a wiring diagram is valid if the monoidal product of elements on the left is less than those on the right.

  • Let’s consider the properties of the order structure:

    • Reflexivity: a diagram consisting of just one wire is always valid.

    • Transitivity: diagrams can be connected together if outputs = inputs

    • Monotonicity: Stacking two valid boxes in parallel is still valid.

    • Unitality: We need not worry about \(I\) or blank space

    • Associativity: Need not worry about building diagrams from top-to-bottom or vice-versa.

    • Symmetry: A diaagram is valid even if its wires cross.

  • One may regard crossing wires as another icon in the iconography.

  • Wiring diagrams can be thought of as graphical proofs

    • If subdiagrams are true, then the outer diagram is true.

Applied examples(1)

  • Resource theories:

    • As discussed here, we consider ’static’ notions.

    • Chemistry: reactants + catalyst \(<\) products + catalyst

    • Manufacturing: you can trash anything you want, and it disappears from view (requires \(\forall x: x \leq I\))

    • Informatics: in addition to trashing, information can be copied (requires \(x \leq x + x\))

Abstract examples(18)

  • Booleans important for the notion of enrichment.

    • Enriching in a symmetric monoidal preorder \(\mathcal{V}=(V,\leq,I,\otimes)\) means "letting \(\mathcal{V}\) structure the question of getting from a to b"

    • Consider \(\mathbf{Bool}=(\mathbb{B},\leq,true,\land)\)

      • The fact that the underlying set is \(\{false, true\}\) means that “getting from a to b is a true/false question"

      • The fact that \(true\) is the monoidal unit translates to the saying “you can always get from a to a"

      • The fact that \(\land\) is the moniodal product means “if you can get from a to b and b to c then you can get from a to c"

      • The ‘if ... then ...’ form of the previous sentence is coming from the order relation \(\leq\).

Opposite SMP(2)

The opposite of a symmetric monoidal preorder \((X, \geq, I, \otimes)\) is still a symmetric monoidal preorder

Proof(1)

  • Monotonicity: \(x_1 \geq y_1 \land x_2 \geq y_2 \implies x_1 \otimes x_2 \geq y_1 \otimes y_2\)

    • This holds because monotonicity holds in the original preorder (\(a\geq b \equiv b \leq a\)).

  • Unitality, symmetry, and associativity are not affected by the preorder.

Natural numbers SMP(1)

There is a symmetric monoidal structure on \((\mathbb{N}, \leq)\) where the monoidal unit is zero and the product is \(+\) (\(6+4=10\)). Monotonicity (\((x_1,x_2)\leq(y_1,y_2) \implies x_1+x_2 \leq y_1+y_2\)) and other conditions hold.

Divisibility SMP(1)

  • Recall the divisibility order \((\mathbb{N}, |)\)

  • There is a symmetric monoidal structure on this preorder with unit \(1\) and product \(*\).

  • Monotonicity (\(x_1|y_1 \land x_2|y_2 \implies x_1*x_2 | y_1*y_2\)) and other conditions hold.

Cost SMP(1)

  • Lawvere’s symmetric monoidal preorder, Cost.

  • Let \([0,\infty]\) represent the non-negative real numbers with infinity. Also take the usual notion of \(\geq\).

  • There is a monoidal structure for this preorder: \(\mathbf{Cost}:=([0,\infty],\geq,0,+)\)

    • The monoidal unit being zero means “you can get from a to a at no cost."

    • The product being + means “getting from a to c is at most the cost of a to b plus b to c"

    • The ‘at most’ above comes from the \(\geq\).

Linked by

Exercise 2-31(2)

Show there is a symmetric monoidal structure on \((\mathbb{N}, \leq)\) where the monoidal product is \(6*4=24\). What should the monoidal unit be?

Solution(1)

  • Let the monoidal product be the standard product for integers, with 1 as unit.

    • Monotonicity: \((x_1,x_2)\leq (y_1,y_2) \implies x_1x_2 \leq y_1y_2\)

    • Unitality: \(1*x_1=x_1=x_1*1\)

    • Associativity: \(a*(b*c)=(a*b)*c\)

    • Symmetry: \(a*b=b*a\)

Exercise 2-33(2)

Recall the divisibility order \((\mathbb{N}, |)\). Someone proposes \((0,+)\) as the monoidal unit and product. Does this satisfy the conditions of a symmetric monoidal structure?

Solution(1)

Conditions 2-4 are satisfied, but not monotonicity: \(1|1 \land 2|4\) but not \(3 | 5\)

Exercise 2-34(2)

  • Consider the preorder defined by the Hasse diagram \(\boxed{no \rightarrow maybe \rightarrow yes}\)

  • Consider a potential monoidal structure with \(yes\) as the unit and \(min\) as the product.

  • Fill out a reasonable definition of \(min\) and check that it satisfies the conditions.

Solution(1)
\(min\) no maybe yes
no no no no
maybe no maybe maybe
yes no maybe yes

  • Monotonicity: \(x_1 \leq y_1 \land x_2 \leq y_2 \implies x_1x_2 \leq y_1y_2\)

    • Suppose without loss of generality that \(x_1\leq x_2\)

    • then \(x_1x_2=x_1\) and \(y_1y_2 = y_1\) or \(y_2\)

    • In the first case, we know this is true because we assumed \(x_1 \leq y_1\)

    • In the second case, we know it from transitivity: \(x_1 \leq x_2\leq y_2\)

  • Unitality: \(min(x,yes)=x\)

  • Associativity: probably

  • Symmetry: table is symmetric.

Linked by

Exercise 2-35(2)

Check that there is a symmetric monoidal structure on the power set of \(S\) ordered by subset relation. (The unit is \(S\) and product is \(\cap\))

Solution(1)

  • Monotonicity: \(x_1 \subseteq y_1 \land x_2 \subseteq y_2 \implies x_1 \cap x_2 \subseteq y_1 \cap y_2\)

    • This is true: if something is in both \(x_1,x_2\), then it is in both \(y_1,y_2\), i.e. in their intersection.

  • Unitality: \(x \cap S = x = S \cap x\), since \(\forall x \in P(S): x \subseteq S\).

  • Associativity and symmetry come from associativity and symmetry of \(\cap\) operator.

Exercise 2-36(2)

  • Let \(Prop^\mathbb{N}\) be the set of all mathematical statements one can make about a natural number.

  • Examples:

    • n is a prime

    • n = 2

    • \(n \geq 11\)

  • We say \(P \leq Q\) if for all \(n \in \mathbb{N}\), \(P(n) \implies Q(n)\)

  • Define a monoidal unit and product on \((Prop^\mathbb{N}, \leq)\).

Solution(1)

  • Let the unit be \(\lambda x. true\) and product be \(\land\)

  • montonicity: \(P_1(x)\leq Q_1(x) \land P_2(x) \leq Q_2(x) \implies (P_1 \land P_2)(x) \leq (Q_1 \land Q_2)(x)\)

    • If the \(P\) properties hold for a given number, then each of the \(Q\) properties hold

  • unitality, associativity, symmetry: same as \(\mathbf{Bool}\)

Exercise 2-40(2)

Consider \(\mathbf{Cost}^{op}\). What is it as a preorder? What is its unit and product?

Solution(1)

As a preorder, the domain is still \([0,\infty]\) and ordered by the natural \(\leq\) relation. The unit and product are unchanged by taking the opposite preorder, so they are still \(0, +\) respectively.

Monoidal monotone maps(9)

Monoidal montones are examples of monoidal functors, specifically lax ones. Oplax functors are a dual notion which has the inequalities reversed.

Monoidal monotone(1)

A monoidal monotone map from \((P,\leq_P,I_P,\otimes_P)\) to \((Q, \leq_Q,I_Q,\otimes_Q)\). Also, a strong monoidal monotone map and a strict monoidal monotone map

  • A monotone map \((P,\leq_P) \xrightarrow{f} (Q,\leq_Q)\) satsifying two conditions:

    1. \(I_Q \leq_Q f(I_P)\)

    2. \(\forall p_1,p_2 \in P:\) \(f(p_1)\ \otimes_Q\ f(p_2)\ \leq_Q\ f(p_1\ \otimes_P\ p_2)\)

  • If the \(\leq\) are replaced with \(\cong\), the map is strong, and if replaced with \(=\), it is strict.

Linked by

Natural Real monoidal monotones(1)

  • Strict monoidal monotone injection \((\mathbb{N},\leq, 0, +) \xhookrightarrow{i} (\mathbb{R},\leq,0,+)\)

  • There is also a monoidal monotone \((\mathbb{R}^+,\leq, 0, +) \xrightarrow{\lfloor x \rfloor} (\mathbb{N},\leq,0,+)\)

    • Monotonic: \(x \leq_\mathbb{R} y \implies \lfloor x \rfloor \leq \lfloor y \rfloor\)

    • But it is neither strict nor strong: \(\lfloor 0.5 \rfloor + \lfloor 0.5 \rfloor \not \cong \lfloor 0.5+0.5 \rfloor\)

Exercise 2-43(2)

Consider a proposed monoidal monotone \(\mathbf{Bool}\xrightarrow{g}\mathbf{Cost}\) with \(g(false)=\infty, g(true)=0\)

  • Check that the map is monotonic and that it satisfies both properties of monoidal monotones.

  • Is g strict?

Solution(1)

  • It is monotonic: \(\forall a,b \in \mathbb{B}: a\leq b \implies g(a)\leq g(b)\)

    • there is only one nonidentity case in \(\mathbf{Bool}\) to cover, and it is true that \(\infty\ \leq_\mathbf{Cost}\ 0\).

  • Condition on units: \(0 \leq_\mathbf{Cost} g(true)\) (actually, it is equal)

  • In \(\mathbf{Cost}\): \(g(x) + g(y) \geq g(x \land y)\)

    • if both true/false, the equality condition holds.

    • If one is true and one is false, then LHS and RHS are \(\infty\) (as \(x \land y = False\)).

  • Therefore this is a strict monoidal monotone.

Exercise 2-44(2)

  • Consider the following functions \(\mathbf{Cost} \xrightarrow{d,u} \mathbf{Bool}\)

    • \(d(x>0)\mapsto false,\ d(0)\mapsto true\)

    • \(u(x=\infty)\mapsto false,\ d(x < \infty) \mapsto true\)

  • For both of these, answer:

    1. Is it monotonic?

    2. If so, does it satsify the monoidal monotone properties?

    3. If so, is it strict?

Solution(1)

  • The function \(d\) asks “Is it zero?”, and the function \(u\) asks “Is it finite?”.

  • Both of these questions are monotone: as we traverse forward in \(\leq_{Cost}\), we traverse towards being zero or being finite.

  • The first monoidal monotone axiom is satisifed in both because the unit (\(0\)) is mapped to the unit (\(True\)).

  • The second monoidal monotone axiom holds for both because addition preserves both things being zero (or not) and both things being finite (or not).

  • These are strict because, in \(Bool\), equality and congruence coincide.

Linked by

Exercise 2-45(2)

  1. Is \((\mathbb{N},\leq,1,*)\) a symmetric monoidal preorder?

  2. If so, does there exist a monoidal monotone \((\mathbb{N},\leq,0,+) \rightarrow (\mathbb{N},\leq,1,*)\)

  3. Is \((\mathbb{Z},\leq,*,1)\) a symmetric monoidal preorder?

Solution(1)

  1. Yes. Monotonicity holds, and multiplication by 1 is unital. The operator is symmetric and associative.

  2. Exponentiation (say, by \(2\)) is a strict monoidal monotone.

    • \(1 = 2^0\) and \(2^x * 2^y = 2^{x+y}\)

  3. No: monotonicity does not hold (multiplying negative numbers gives a larger number).

Enrichment(20)
V-categories(2)
V-category(1)

A \(\mathcal{V}\) category, given a symmetric monoidal preorder \(\mathcal{V}=(V,\leq,I,\otimes)\)

  • To specify the category \(\mathcal{X}\), one specifies:

    1. A set \(Ob(\mathcal{X})\) whose elements are called objects

    2. A hom-object for every pair of objects in \(Ob(\mathcal{X})\), written \(\mathcal{X}(x,y) \in V\)

  • The following properties must be satisfied:

    1. \(\forall x \in Ob(\mathcal{X}):\) \(I \leq \mathcal{X}(x,x)\)

    2. \(\forall x,y,z \in Ob(\mathcal{X}):\) \(\mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)

  • We call \(\mathcal{V}\) the base of enrichment for \(\mathcal{X}\) or say that \(\mathcal{X}\) is enriched in \(\mathcal{V}\).

Linked by

Bool-category(1)

  • Consider the following preorder:

  • As a Bool-category, the objects are \(Ob(\mathcal{X})=\{p,q,r,s,t\}\).

    • For every pair, we need an element of Bool, so make it true if \(x\leq y\)

    • \(true\) is the monoidal unit of Bool, and this obeys the two constraints of a \(\mathcal{V}\) category.

  • We can represent the binary relation (hom-object) with a table:

    \(\leq\) p q r s t
    p T T T T T
    q F T F T T
    r F F T T T
    s F F F T T
    t F F F F T

Preorders as Bool-categories(2)
Preorders are Bool-categories(2)

There is a one-to-one correspondence between preorders and Bool-categories

Proof(1)

  • Construct preorder \((X,\leq_X)\) from any Bool-category \(\mathcal{X}\)

    • Let \(X\) be \(Ob(\mathcal{X})\) and \(x\ \leq_X\ y\) be defined as \(\mathcal{X}(x,y)=true\)

    • This is reflexive and transitive because of the two constraints we put on enriched categories.

      • The first constraint says that \(true \leq (x \leq_X x)\)

      • The second constraint says \((x \leq_X y) \land (y \leq_X z) \leq (x \leq_X z)\)

  • Construct Bool-category from a preorder:

    • Let \(Ob(X)=X\) and define \(\mathcal{X}(x,y)=true\) iff \(x \leq_X y\)

    • The two constraints on preorders give us our two required constraints on enriched categories.

Lawvere metric spaces(10)

  • Can convert any weighted graph into a Lawvere metric space, where a the distance is the sum of weights along the shortest path.

  • It can be hard to see the shortest path by inspection, but a matrix power iteration method (starting from just a matrix of edge weights) is possible.

Metric space(1)

A metric space \((X,d)\)

  • A set \(X\) whose elements are called points

  • A function \(X \times X \xrightarrow{d} \mathbb{R}_{\geq 0}\) which gives the distance between two points.

  • These must satisfy three properties:

    1. \(d(x,y)=0 \iff x=y\)

    2. \(d(x,y)=d(y,x)\)

    3. \(d(x,y)+d(y,z)\geq d(x,z)\) (triangle inequality)

  • An extended metric space includes \(\infty\) in the codomain of the cost function.

Linked by

Lawvere metric space(1)

A Lawvere metric space

  • A Cost-category, i.e. a category enriched in the symmetric monoidal preorder \(\mathbf{Cost}=([0,\infty],\geq,0,+)\).

  • \(X\) is given as \(Ob(\mathcal{X})\)

  • \(d(x,y)\) is given as \(\mathcal{X}(x,y)\)

  • The axiomatic properties of a category enriched in Cost are:

    • \(0 \geq d(x,x)\)

    • \(d(x,y)+d(y,z) \geq d(x,z)\)

Linked by

Reals metric space(1)

The set \(\mathbb{R}\) can be given a metric space structure, with \(d(x,y)=|x-y|\).

Exercise 2-52(2)

  • Imagine the points of a metric space are whole regions, like US, Spain, and Boston. Distance is "Given the worst case scenario, how far do you have to travel to get from region A to B?"

  • This actually breaks our symmetry requirement: \(d(Boston,US)=0, d(US,Boston) > 0\)

  • Which distance is bigger in this framework: \(d(Spain,US)\) or \(d(US,Spain)\)?

Solution(1)

  • \(d(US,Spain)\) is bigger because there is much more room for the worst case scenario to place one farther for Spain.

  • A bigger first argument makes things strictly worse, all else equal. A bigger second argument makes things strictly better, all else equal.

Linked by

Exercise 2-55(2)

Consider the symmetric monoidal preorder \((\mathbb{R},\geq,0,+)\) which is the same as Cost but does not include \(\infty\). How do you characterize the difference between this and a Lawvere metric space in the sense of definition 2.46?

Solution(1)

It is a metric space in which points may only be finitely-far apart.

Exercise 2-60(2)

What is the distance matrix represented by this graph?

Solution(1)
\(\rightarrow\) A B C D
A 0 6 3 11
B 2 0 5 5
C 5 3 0 8
D 11 9 6 0

Linked by

V-variations on preorders and metric spaces(6)
Exercise 2-61(2)

Recall the symmetric monoidal preorder \(\mathbf{NMY} := (P,\leq, yes, min)\) from Exercise 2.34. Interpret what a NMY-category is.

Solution(1)

It is like a graph where some edges are ‘maybe’ edges. We can ask the question “Is there a path from a to b?" and if there is a true path we will get a ‘yes’. If the only paths are those which include maybe edges, then we get a ’maybe’. If there’s no path at all, we get a ‘no’.

Exercise 2-62(2)

  • Let \(M\) be a set and \(\mathcal{M}:=(P(M),\subseteq, M, \cap)\) be the symmetric monoidal preorder whose elements are subsets of \(M\).

  • Someone says "for any set \(M\), imagine it as the set of modes of transportation (e.g. car, boat, foot)". Then an \(\mathcal{M}\) category \(\mathcal{X}\) tells you all the modes that will get you from a all the way to b, for any two points \(a,b \in Ob(\mathcal{X})\)

    1. Draw a graph with four vertices and five edges, labeled with a subset of \(M=\{car,boat,foot\}\)

    2. From this graph it is possible to construct an \(\mathcal{M}\) category where the hom-object from x to y is the union of the sets for each path from x to y, where the set of a path is the intersection of the sets along the path. Write out the corresponding 4x4 matrix of hom-objects and convince yourself this is indeed an \(\mathcal{M}\) category.

    3. Does the person’s interpretation look right?

Solution(1)

  1. (implicitly, no path means edge of \(\varnothing\) and self paths are \(cfb\))

  2. Hom objects:

    A B C D
    A cbf cbf cf cf
    B \(\varnothing\) cbf \(\varnothing\) c
    C \(\varnothing\) \(\varnothing\) cbf bf
    D \(\varnothing\) \(\varnothing\) \(\varnothing\) cbf

    • The first property (\(\forall x \in Ob(\mathcal{X}): I \leq \mathcal{X}(x,x)\)) is satisfied by noting the diagonal entries are equal to the unit.

    • The second property (\(\forall x,y,z \in Ob(\mathcal{X}): \mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)) can be checked looking at the following cases:

      • \(A \rightarrow B \rightarrow D\): \(cbf \cap c \leq cf\)

      • \(A \rightarrow C \rightarrow D\): \(cf \cap bf \leq cf\)

  3. One subtlety is that we need to say that one can get from any place to itself by any means of transportation for this to make sense. Overall interpretation looks good.

Exercise 2-63(2)

Consider the symmetric monoidal preorder \(\mathcal{W}:=(\mathbb{N}\cup\{\infty\},\leq,\infty,min)\)

  1. Draw a small graph labeled by elements of \(\mathbb{N}\cup\{\infty\}\)

  2. Write a the matrix whose rows and columns are indexed by nodes in the graph, whose (x,y)th entry is given by the maximum over all paths p from x to y of the minimum edge label in p.

  3. Prove that this matrix is a matrix of hom-objects for a \(\mathcal{W}\) category called \(\mathcal{X}\).

  4. Make up an interpretation for what it means to enrich in \(\mathcal{W}\)

Solution(1)

  1. (implicitly, no path means path of weight 0, and self paths have weight \(\infty\))

  2. Maxmin matrix:

    A B C D
    A \(\infty\) 3 \(\infty\) 3
    B 0 \(\infty\) 0 \(\infty\)
    C 0 3 \(\infty\) 3
    D 0 1 0 \(\infty\)

    Self paths are equal to the monoidal unit and it will never be the case that \(min(\mathcal{X}(A,B),\mathcal{X}(B,C)) > \mathcal{X}(A,C)\) because even in the worst-case scenario (where there is not a better path from A to C that ignores B completely), we form the best path by combining the best path from A to B with the best from B to C. We are forced to take the minimum edge label in the path, which means that the lowest \(\mathcal{X}(A,C)\) can be is actually equal to the left hand side.

  3. The edges could represent constraints (\(\infty\) is fully unconstrained, \(0\) is fully constrained, e.g. the diameter of a pipe) and the hom-object represents the least-constrained thing that can get from one point to another. The monoidal unit says that something can be fully unconstrained if it stays where it is, and the monoidal product (min) says how to compose two different constraints in series.

Constructions on V-categories(18)
Changing the base of enrichment(7)
Induced V-categories from monoidal monotones(2)

Let \(\mathcal{V}\xrightarrow{f}\mathcal{W}\) be a monoidal monotone map. Given a \(\mathcal{V}\) category, called \(\mathcal{C}\), one can construct an associated \(\mathcal{W}\) category, let’s call it \(\mathcal{C}_f\)

Proof(1)

  • Take the same objects: \(Ob(\mathcal{C}_f):=Ob(\mathcal{C})\)

  • \(\mathcal{C}_f(a,b) := f(\mathcal{C}(a,b))\)

  • Check this obeys the definition of an enriched category:

    • Condition on the monoidal unit:

      1. \(I_W \leq f(I_V)\) — from the first condition of a monoidal monotone map.

      2. \(\forall c \in Ob(\mathcal{C}): I_V \leq \mathcal{C}(c,c)\) — first condition of an enriched category, which \(\mathcal{C}\) is

      3. \(\forall c \in Ob(\mathcal{C}):f(I_V) \leq f(\mathcal{C}(c,c))\) — monotone map property

      4. \(\forall c \in Ob(\mathcal{C}):f(I_V) \leq \mathcal{C}_f(c,c)\) — definition of \(\mathcal{C}_f\)

      5. \(\forall c \in Ob(C_f): I_W \leq C_f(c,c)\) — transitivity, using 1 and 4, noting \(Ob(\mathcal{C})=Ob(\mathcal{C}_f)\)

    • Condition on monoidal product:

      1. \(\mathcal{C}_f(c,d) \otimes_W \mathcal{C}_f(d,e) = f(\mathcal{C}(c,d)) \otimes_W f(\mathcal{C}(d,e))\) — definition of \(\mathcal{C}_f\)

      2. \(f(\mathcal{C}(c,d)) \otimes_W f(\mathcal{C}(d,e)) \leq f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e))\) — second condition of a monoidal monotone map

      3. \(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e) \leq \mathcal{C}(c,e)\) — Second condition of an enriched category

      4. \(f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e)) \leq f(\mathcal{C}(c,e)\) — monotone map property

      5. \(f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e)) \leq \mathcal{C}_f(c,e)\) — definition of \(\mathcal{C}_f\)

      6. \(\mathcal{C}_f(c,d) \otimes_W \mathcal{C}_f(d,e) \leq \mathcal{C}_f(c,e)\) — transitivity, 1,2 and 5

Linked by

Metric space to preorder(1)

  • Consider the function \([0,\infty] \xrightarrow{f} \mathbb{B}\) which maps 0 to true and otherwise to false.

  • Can check that f is monotonic and preserves the monoidal product+unit, so it is a monoidal monotone. (this was shown in Exercise 2.44)

  • Thus we have a tool to convert metric spaces into preorders.

Linked by

Exercise 2-67(2)

Recall the “regions of the world” Hausdorff metric space We learned that a metric space can be converted into a preorder by a particular monoidal monotone map. How would you interpret the resulting preorder?

Solution(1)

The edges in the preorder represent the \(\subseteq\) relation. For Boston, US, and Spain, it would look like this (with implicit self-edges):

Exercise 2-68(2)

Find a different monoidal monotone map \(\mathbf{Cost}\xrightarrow{g}\mathbf{Bool}\) from the one in Example 2.65. Using the construction from Proposition 2.64, convert a Lawvere metric space into two different preorders. Find a metric space for which this happens.NOCARD

Solution(1)
Enriched functors(5)
V-functor(1)

A \(\mathcal{V}\) functor \(\mathcal{X}\xrightarrow{F}\mathcal{Y}\) between two \(\mathcal{V}\) categories

A function \(Ob(\mathcal{X})\xrightarrow{F}Ob(\mathcal{Y})\) subject to the constraint:

  • \(\forall x_1,x_2 \in Ob(\mathcal{X}): \mathcal{X}(x_1,x_2) \leq \mathcal{Y}(F(x_1),F(x_2))\)

Linked by

Bool-functors(1)

  • Monotone maps, considering the source and target preorders as Bool-categories, are in fact Bool-functors.

  • The monotone map constraint, that \(x_1\ \leq_X\ x_2 \implies F(x_1)\leq_Y F(x_2)\), translates to the enriched category functor constraint, that \(\mathcal{X}(x_1,x_2) \leq \mathcal{Y}(F(x_1),F(x_2))\).

Cost-functors(1)

  • A Cost-functor is also known as a Lipschitz function.

  • Therefore a Lipschitz function is one under which the distance between any pair of points does not increase.

Exercise 2-73(2)

  • The concepts of opposite/dagger/skeleton extend from preorders to \(\mathcal{V}\) categories.

    • An opposite \(\mathcal{V}\) category \(\mathcal{X}\) has the same objects and \(\mathcal{X}^{op}(x,y):=\mathcal{X}(y,x)\)

    • A dagger category is identical to its opposite.

    • A skeletal \(\mathcal{V}\) category is one in which \(I \leq \mathcal{X}(x,y) \land I \leq \mathcal{X}(y,x)\) implies \(x = y\)

  • Recall an extended metric space \((X,d)\) is a Lawvere metric space with two extra properties.

  • Show that a skeletal dagger Cost-category is an extended metric space

Solution(1)

  • The skeletal dagger cost category has a set of objects, \(Ob(\mathcal{X})\) which we can call points.

  • For any pair of points, we assign a hom-object in \([0,\infty]\) (we can call this a distance function).

  • Skeletal property enforces the constraint \(d(x,y)=0 \iff x=y\).

  • The second enriched category property enforces the triangle inequality.

  • Because we have a dagger category, our distance function is forced to be symmetric.

  • Just like the information of a preorder is discarded (to yield a set) when we only consider skeletal dagger preorders, information must be discarded from Cost-categories to yield a Lawvere metric space.

Linked by

Product V-categories(6)
V-category product(1)

The \(\mathcal{V}\) product of two \(\mathcal{V}\) categories, \(\mathcal{X} \times \mathcal{Y}\)

This is also a \(\mathcal{V}\) category with:

  1. \(Ob(\mathcal{X}\times\mathcal{Y}) := Ob(\mathcal{X})\times Ob(\mathcal{Y})\)

  2. \((\mathcal{X} \times \mathcal{Y})((x,y),(x',y')) := \mathcal{X}(x,x') \otimes \mathcal{Y}(y,y')\)

Linked by

Cost-category product(1)

  • Let \(\mathcal{X}\) and \(\mathcal{Y}\) be the Lawvere metric spaces (i.e. Costcategories) defined by the following weighted graphs.

  • The product can be represented by the following graph:

  • The distance between any two points \((x,y),(x',y')\) is given by the sum \(d_X(x,x)+d_Y(y,y)\).

  • We can also consider the Cost-categories as matrices

    \(\mathcal{X}\) A B C
    A 0 2 5
    B \(\infty\) 0 3
    C \(\infty\) \(\infty\) 0
    \(\mathcal{Y}\) P Q
    P 0 5
    Q 8 0
    \(\mathcal{X}\times\mathcal{Y}\) (A,P) (B,P) (C,P) (A,Q) (B,Q) (C,Q)
    (A,P) 0 2 5 5 7 10
    (B,P) \(\infty\) 0 3 \(\infty\) 5 8
    (C,P) \(\infty\) \(\infty\) 0 \(\infty\) \(\infty\) 5
    (A,Q) 8 10 13 0 2 5
    (B,Q) \(\infty\) 8 11 \(\infty\) 0 3
    (C,Q) \(\infty\) \(\infty\) 8 \(\infty\) \(\infty\) 0

  • Can view this as a 2x2 grid of 3x3 blocks: each is a \(\mathcal{X}\) matrix shifted by \(\mathcal{Y}\).

Exercise 2-75(2)

Let \(\mathcal{X} \times \mathcal{Y}\) be the \(\mathcal{V}\)-product of two \(\mathcal{V}\) categories.

  1. Check that for every object we have \(I \leq (\mathcal{X} \times \mathcal{Y})((x,y),(x,y))\)

  2. Check that for every three objects we have:

    • \((\mathcal{X} \times \mathcal{Y})((x_1,y_1),(x_2,y_2)) \otimes (\mathcal{X} \times \mathcal{Y})((x_2,y_2),(x_3,y_3)) \leq (\mathcal{X} \times \mathcal{Y})((x_1,y_1),(x_3,y_3))\)

Solution(1)

    • By axioms of \(\mathcal{V}\) categories: \(I \leq \mathcal{X}(x,x')=xx\) and \(I \leq \mathcal{Y}(y,y')=yy\)

    • By monotonicity: \(I \leq xx \land I \leq yy\) implies \(I = I \otimes I \leq xx \otimes yy\).

    • By the definition of a product category this last term can be written as \((\mathcal{X} \times \mathcal{Y})((x,y),(x,y))\)

    • By axioms of \(\mathcal{V}\) categories: \(\mathcal{X}(x_1,x_2) \otimes \mathcal{X}(x_2,x_3) \leq \mathcal{X}(x_1,x_3)\) and \(\mathcal{Y}(y_1,y_2) \otimes \mathcal{Y}(y_2,y_3) \leq \mathcal{Y}(y_1,y_3)\)

    • Therefore, by monotonicity, we have \((\mathcal{X}(x_1,x_2) \otimes \mathcal{X}(x_2,x_3)) \otimes (\mathcal{Y}(y_1,y_2) \otimes \mathcal{Y}(y_2,y_3)) \leq \mathcal{X}(x_1,x_3) \otimes \mathcal{Y}(y_1,y_3)\)

    • Desugaring the definiton of the hom-object in \(\mathcal{X}\times\mathcal{Y}\), the property we need to show is that \((\mathcal{X}(x_1,x_2) \otimes\mathcal{Y}(y_1,y_2)) \otimes (\mathcal{X}(x_2,x_3) \otimes\mathcal{Y}(y_2,y_3)) \leq (\mathcal{X}(x_1,x_3) \otimes\mathcal{Y}(y_1,y_3))\)

    • Given the associativity and commutitivity of the \(\otimes\) operator, we can rearange the order and ignore parentheses for the four terms on the LHS. Do this to yield the desired expression.

Exercise 2-78(2)

  • Consider \(\mathbb{R}\) as a Lawvere metric space, i.e. as a Cost-category.

  • Form the Cost-product \(\mathbb{R}\times\mathbb{R}\).

  • What is the distance from \((5,6)\) to \((-1,4)\)?

Solution(1)

The distance is the Manhattan/\(L_1\) distance: \(|5-(-1)| + |6-4| = 8\)

Computing presented V-categories with matrix mult(33)
Monoidal closed preorders(11)

  • The term closed in the context of symmetric monoidal closed preorders refers to the fact that a hom-element can be constructed from any two elements (the preorder is closed under the operation of "taking homs").

  • Consider the hom-element \(v \multimap w\) as a kind of "single use v to w converter"

    • a and v are enough to get to w iff a is enough to get to a single-use v-to-w converter.

  • One may read

    • P2.87c as saying "if I have a v and a single-use v to w converter, then I have a w" and

    • P2.87d as saying "Having v is the same as shaving a single-use nothing-to-v converter"

    • P2.87e as saying "We can compose two single-use converters"

Closed SMP(1)
Self-enriched category(1)

A category \(\mathcal{V}\) that is enriched in itself.

  • For every \(v,w \in Ob(\mathcal{V})\) we can define \(\mathcal{V}(v,w)\) as \((v \multimap w) \in \mathcal{V}\)

  • For this to be an enrichment, we need to check the two conditions.

    • The first condition \(I \leq \mathcal{X}(x,x) = x \multimap x\) is satsified because \(I \otimes x \leq x\)

    • The second condition is satisfied by P2.87e

Linked by

Cost is closed(1)

  • The symmetric monoidal preorder \(\mathbf{Cost}:=([0,\infty],\geq,0,+)\) is monoidal closed.

  • For any \(x,y \in [0,\infty]\), define \(x \multimap y := max(0,y-x)\)

  • Then, for any \(a,x,y\), we have \(a+x\geq y\) iff \(a \geq y-x\) iff \(max(0,a)\geq max(0,y-x)\) iff \(a \geq (x \multimap y)\)

  • We can use this to define a notion of subtraction in Cost.

Linked by

Chemistry closed resource theory(1)

  • What would a monoidal closed structure mean for the resource theory of chemistry?

  • For any two material collections, one can form a material collection \(c \multimap d\) with the property that, for any a one has \(a + c \rightarrow d\) iff \(a \rightarrow (c \multimap d)\)

  • Concretely, say we have \(2 H_2O + 2 Na \rightarrow 2 NaOH + H_2\), we must also have \(2H_2O \rightarrow (2Na \multimap (2NaOH+H_2))\)

  • From two molecules of water, you can form a certain substance. This doesn’t make sense, so maybe this symmetric monoidal preorder is not closed.

  • Alternatively, think of the substance \(2Na \multimap (2NaOH+H_2)\) as a potential reaction, that of converting sodium to sodium-hyroxide+hydrogen. Two molecules of water unlock that potential. NOCARD

SMP currying(2)
Proof(1)

  • The meaning of \((- \otimes v) \dashv (v \multimap -)\) is exactly the condition of \(\multimap\) in a closed symmetric monoidal preorder.

  • This follows from (1), using the fact that left adjoints preserve joins.

  • This follows from (1) using the alternative characterization of Galois connections.

    • Alternatively, start from definition of closed symmetric monoidal preorder and substitute \(v \multimap w\) for \(a\), and note by reflexivity that \((v \multimap w) \leq (v \multimap w)\)

    • Then we obtain \((v \multimap w) \otimes v \leq w\) (by symmetry of \(\otimes\) we are done)

  • Since \(v \otimes I = v \leq v\), then the closed condition means that \(v \leq I \multimap v\)

    • For the other direction, we have \(I \multimap v = I \otimes (I \multimap v) \leq v\) by (3)

  • We need \(u \otimes (u \multimap v) \otimes (v \multimap w) \leq w\)

    • This follows from two applications of the third part of this proposition.

Suppose \(\mathcal{V}:=(V,\leq,I,\otimes,\multimap)\) is a closed symmetric monoidal preorder.

  • For every \(v \in V\) the monotone map \((V, \leq) \xrightarrow{-\otimes v}(V,\leq)\) is left adjoint to \((V, \leq)\ \xrightarrow{v \multimap -} (V,\leq)\)

  • For any element \(v \in V\) and a subset of elements \(A \subseteq V\), if the join \(\bigvee A\) exists, then so does \(\bigvee_{a \in A} v \otimes a\) and we have \((v \otimes \bigvee A)\cong \bigvee_{a \in A} v \otimes a\)

  • \(\forall v,w \in V: v \otimes (v \multimap w) \leq w\)

  • \(\forall v \in V: v \cong (I \multimap v)\)

  • \(\forall u,v,w \in V: (u \multimap v) \otimes (v \multimap w) \leq (u \multimap w)\)

Linked by

Exercise 2-82(2)

Prove that a symmetric monoidal preorder is closed iff, given any \(v \in V\), the map \(V \xrightarrow{(-\otimes v)}V\) given by multiply with v has a right adjoint. We write this adjoint \(V \xrightarrow{(v \multimap -)}V\):

  1. Show that \(V \xrightarrow{(-\otimes v)}V\) is monotone.

  2. Supposing that \(\mathcal{V}\) is closed, show that \(\forall v,w \in V: ((v \multimap w)\otimes v) \leq w\)

  3. Show that \((v \multimap -)\) is monotone.

  4. Conclude that a symmetric monoidal preorder is closed iff the monotone map \((- \otimes v)\) has a right adjoint.

Solution(1)

    • Given the monotonicity constraint of \(\otimes\)

    • And reflexivity: \(v \leq v\), we have:

    • \(x_1 \leq y_1\) implies that \((x_1 \otimes v) \leq (y_1 \otimes v)\)

  2. Substitute \(v \multimap w\) for \(a\) into the closed property equation, to get \(((v \multimap w)\otimes v) \leq w \iff v \multimap w \leq v \multimap w\) (the RHS is true by reflexivity, so the LHS must be true).

  3. Need to show: if we assume \(x \leq y\) then we can conclude \((v \multimap x) \leq (v \multimap y)\)

    • From the previous part, we have \((v \multimap x) \otimes v \leq x\) and \((v \multimap y) \otimes v \leq y\)

    • Assuming the antecedant \(x \leq y\), and given transitivity, we have \((v \multimap x) \otimes v \leq (v \multimap y) \otimes v\)

    • Because the \(\otimes\) operation must be monotonic, the consequent follows.

  4. A Galois connection requires that both maps be monotone and that they satisfy \(f(p)\leq q\) iff \(p \leq g(q)\). This is the relation captured by the closed property equation, and both maps were shown to be monotone.

Exercise 2-85(2)

Show that \(\mathbf{Bool}=(\mathbb{B},\leq, true, \land)\) is monoidal closed.

Solution(1)

  • Our translation is: \(\otimes \mapsto \land,\ \leq \mapsto \implies\)

  • Condition for being closed is then:

  • \(\forall a,v,w:\) \((a \land v) \implies w\) iff \(a \implies (v \multimap w)\)

  • On the LHS, we have the truth table:

    a v w \((a \land v) \implies w\)
    F F F T
    F F T T
    F T F T
    F T T T
    T F F T
    T F T T
    T T F F
    T T T T

  • In order to define \(v \multimap w\) in a way consistent with this, we need it to only be false when \(v=true, w=false\), which is the truth condition for \(v \implies w\).

  • This is consistent with a ‘single use v-to-w converter’ analogy.

Linked by

Quantales(13)

  • Think of a unital, commutative, quantale as a kind of navigator.

    • A navigator understands ’getting from one place to another’

    • Different navigators understand different aspects (whether one can get from A to B, how much time it will take, ...)

    • What they share in common is that, given routes A to B and B to C, they understand how to get a route A to C.

  • Because of Proposition 2.96, a quantale has all meets and joins (even though we define it simply as having all joins).

Quantale(1)
Cost quantale(1)

  • We saw that Cost is monoidal closed in Example 2.83

  • To check if Cost is a quantale, we take an arbitrary set of elements and ask if it has a join.

  • Because \(\geq\) is a total order, we can take the infimum or greatest lower bound, as the join.

    • \(\bigvee\{2.5,2.05,2.005,...\} = 2\).

  • We need a \(0\), which is something which is related to everything (the first join condition is vacuous). Because the preorder relation is \(\geq\) in Cost we need something greater than everything, so \(0 = \infty\).

  • Thus Cost is a quantale.

All joins implies all meets(2)

Let \((P,\leq)\) be a preorder. It has all joins iff it has all meets.

Proof(1)

  • Meets and joins are dual, so it suffices to prove one of the directions (the opposite category shows that having all meets having all joins, if we are able to prove that having all joins means having all meets in the original preorder).

  • Suppose there are all joins and \(A \subseteq P\) is a subset for which we want the meet.

  • Consider the set \(M_A := \{p \in P\ |\ \forall a \in A: p \leq a \}\) (everything below all of \(A\) - these are candidates for the meet of \(A\))

  • The first condition for the meet is satisfied by all. We get the actual meet by taking \(\bigvee M_A\) which is guaranteed to exist. Because this element is greater than or equal to all elements that are \(\leq A\), it satisfies the second condition for the meet.

Linked by

Quantale is SMP with all joins(2)

Suppose \(\mathcal{V}=(V,\leq,I,\otimes)\) is a symmetric monoidal preorder that has all joins.

  • Then \(\mathcal{V}\) is closed, i.e. has a \(\multimap\) operation and hence is a quantale, iff \(\otimes\) distributes over joins

  • i.e. if Eq (2) from P2.87 holds: \((v \otimes \bigvee A)\cong \bigvee_{a \in A} v \otimes a\).

Proof(1)

  • We proved one direction in P2.87

  • We need to show that \((v \otimes \bigvee A)\cong \bigvee_{a \in A} v \otimes a\) (and all joins existing) implies that there exists a \(\multimap\) operation that satisfies the closed property: \(\forall a,v,w \in V: (a \otimes v) \leq w\) iff \(a \leq (v \multimap w)\).

  • The adjoint functor theorem for preorders states that monotone maps preserve joins iff they’re left adjoint, so \(V \xrightarrow{-\otimes v} V\) must have a right adjoint g, which, being a Galois connection, will satisfy the property \((a \otimes v) \leq w \iff a \leq g(w)\) (this is the monoidal closed property).

  • Let’s rename \(g \equiv v \multimap -\). The adjoint functor theorem even gives us a construction for the right adjoint, namely: \(v \multimap w:=\bigvee\{a \in V\ |\ a \otimes v \leq w\}\).

Linked by

Exercise 2-92(2)

  1. What is \(\bigvee \varnothing\), called \(0\), in the case of:

    • \(\mathcal{V}=\mathbf{Bool}=\{\mathbb{B},\leq, true,\land\}\)

    • \(\mathcal{V}=\mathbf{Cost}=([0,\infty],\geq,0,+)\)

  2. What is the join \(x \vee y\) for Bool and Cost?

Solution(1)

  1. \(False\) and \(\infty\) respectively

  2. Logical or and \(min\) respectively

Exercise 2-93(2)

Show that Bool is a quantale

Solution(1)

The joins all exist:

  • nontrivial ones: \(\varnothing \mapsto False, \{True,False\}\mapsto True\)

Exercise 2-94(2)

Recall the power set symmetric monoidal preorder \((P(S),\subseteq, S, \cap)\) Is this a quantale?

Solution(1)

Yes, \(0=\varnothing\) (it is related to everything) and the join of any pair of subsets is well-defined as their union. By Proposition 2.98, this means it is a quantale.

Matrix multiplication in a quantale(9)

The identity \(\mathcal{V}\) matrix, \(X \times X \xrightarrow{I_X} \mathcal{V}\) has \(I\) on the diagonal entries and \(0\) on the off-diagonal entries.

Quantale matrix(1)

A matrix with entries in \(\mathcal{V}\), where \(\mathcal{V}=(V, \leq, \otimes, I)\) is a quantale. (A \(\mathcal{V}\) matrix). Matrix multiplication between \(\mathcal{V}\) matrices

  • Need two sets, and function \(X \times Y \xrightarrow{M} V\). Call \(M(x,y)\) the (x,y)th entry.

  • We can multiply \(X \times Y \xrightarrow{M} V\) and \(Y \times Z \xrightarrow{N} V\) to get a new \(\mathcal{V}\) matrix \(X \times Z \xrightarrow{M*N} V\).

    • \((M*N)(x,z)(x,z)\) defined as \(\bigvee_y\ M(x,y)\otimes N(y,z)\)

    • Note that this is similar to the standard matrix multiplication, with \(\bigvee \mapsto \Sigma, \otimes \mapsto *\)*

Linked by

Abstract matrix multiplication(1)

Let \(\mathcal{V}=\mathbf{Bool}\). Here is matrix multiplication \(M*N\) with \(X=\bar{3}, Y=\bar{2},Z=\bar{3},M=X\times Y\rightarrow Z, N=Y\times Z\rightarrow B\).

\(X\)

F F
F T
T T

\(Y\)

T T F
T F T

\(X*Y\)

F F F
T F T
T T T

Exercise 2-103(2)

Write the 2x2 identity matrices for each of the quantales:

  1. \((\mathbb{N},\leq,1,*)\)

  2. \(\mathbf{Bool}:=(\mathbb{B},\leq,true,\land)\)

  3. \(\mathbf{Cost}:=([0,\infty],\leq,0,+)\)

Solution(1)
  1. 1 0
    0 1
  2. T F
    F T
  3. 0 \(\infty\)
    \(\infty\) 0
Exercise 2-104(2)

Let \(\mathcal{V}=(V,\leq,I,\otimes,\multimap)\) be a quantale. Prove:

  1. The identity law

    • For all \(\mathcal{V}\) matrices \(X\times Y\xrightarrow{M}V\), one has \(I_X * M = M\)

  2. The associative law

    • For any matrices \(W \times X \xrightarrow{M} V, X \times Y \xrightarrow{N} V, Y \times Z \xrightarrow{P} V\), one has \((M*N)*P=M*(N*P)\)

Solution(1)

    • \(\forall v \in \mathcal{V}\), we have \(0 \otimes v \cong 0\).

      • \(0 \otimes v\)

      • \(\cong v \otimes 0\) – symmetry

      • \(= v \otimes \bigvee_{a \in \varnothing} a\) – definition of \(0\)

      • \(\cong \bigvee_{a \in \varnothing} v \otimes a\) – \(-\otimes x\) preserves joins b/c it is left adjoint

      • \(= 0\) – definition of 0

    • Plug this into definition of matrix multiplication

      • \(I_X * M(x,y)\)

      • \(= \bigvee_{x'}I_x(x,x')\otimes M(x',y)\) – definition of matrix multiplication in a quantale

      • \(=(I_x(x,x)\otimes M(x,y))\vee(\bigvee_{x'\ne x}I_x(x,x')\otimes M(x',y))\) – split join into two cases

      • \(=(I\otimes M(x,y))\vee(\bigvee_{x'\ne x}0\otimes M(x',y))\) – Definition of identity matrix

      • \(=M(x,y)\vee 0\) – join of a singleton set

      • \(=M(x,y)\) – Zero is the least element in \(\mathcal{V}\)

    • Need to show \(\underset{y \in Y}\bigvee (\underset{x\in X}\bigvee M(w,x)\otimes N(x,y))\otimes P(y,z)\) is the same as \(\underset{x \in X}\bigvee M(w,x)\otimes(\underset{y \in Y}\bigvee N(x,y) \otimes P(y,z))\) for all \(w \in W,z \in Z\)

    • The associativity of \(\otimes\) and the fact it preserves joins b/c it is left adjoint lets us shift the symbols around appropriately.

Linked by

Exercise 2-105(2)

Consider the distance matrix represented by this graph from Exercise 2.60:

\(\rightarrow\) A B C D
A 0 6 3 11
B 2 0 5 5
C 5 3 0 8
D 11 9 6 0

Compute the distance matrix by power iteration of the matrix of the presentation.

Solution(1)
\(M\) A B C D
A 0 \(\infty\) \(\infty\) 3
B 2 0 5 \(\infty\)
C \(\infty\) \(\infty\) 0 6
D \(\infty\) 3 \(\infty\) 0

\(M^2\) A B C D
A 0 6 \(\infty\) 3
B 2 0 5 11
C \(\infty\) 9 0 6
D 5 3 8 0

After this, \(M^n\) is the \(\rightarrow\) matrix